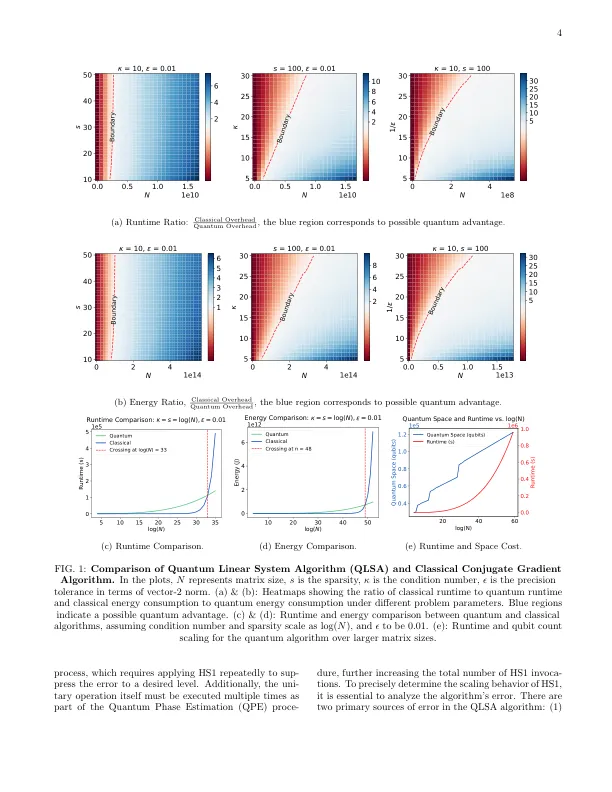
复杂性理论在理论上已经在诸如分解[2],搜索[3]和类似[4]等问题中得到了证明。这些进步为在半导体行业中维持或超越摩尔法律提供了希望。然而,除了从理论计算机科学的栅极模型中估算的时间复杂性之外,它在实践中估算和证明可能的量子可能性是合理的。首先,对量子计算的实用成本估计需要最先进的知识,从涵盖复杂性的详细理论涵盖预先因素[5,6]到量子硬件的明确设计,并且包括更全面的测量,包括更全面的测量值,例如时间成本(以秒为单位)(在第二秒内进行测量),空间成本(数量),零售成本(数量),以及能量成本。,量化能源效率估计的复杂性质是高度未经评估的,尽管量子算法的可能能量优势主要在定性论证中讨论了[7-9]。第二,尽管某些算法的存在量子优势的存在在理论上是坚定合理的,但要证明这些因素可以变成现实世界,这是挑战,对于商业应用而言,尤其是显着的好处[10]。最后,量子状态非常脆弱,当前的量子处理器嘈杂,使量子误差校正是制造大规模,耐断层量子计算的唯一方法。容忍度虽然在理论上可以持续存在,但仍需要许多其他资源和实验挑战,从而使精确的资源估计更具挑战性。因为lin-在这项工作中,我们通过对所谓的Harrow-Hassidim-lloyd(HHL)算法进行全面的,能源感知的资源估算来解决这些挑战[11]。HHL算法提供了可用于求解线性代数问题的量子线性系统算法(QLSA)。给定线性方程式A | x⟩= | b⟩,该算法返回量子状态| X = A - 1 | B⟩作为解决方案。对于某些类别的矩阵,已经表明,该算法在poly(log n)的时间为n×n矩阵以poly(log n)时间运行,这使其比任何已知的经典对应物都要快。复杂性 - 理论论点还表明,某些设置是BQP填充的算法[11]。
Finllama:算法交易申请的财务情感分类
主要关键词